ALTIN ORAN

Altın Oran

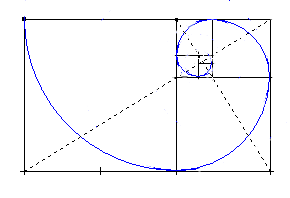
Bu karelerin kenar uzunlukları sırasıyla Fibonacci sayılarını verir.

Altın orana ilişkin matematik bilgisi ilk kez İ.Ö. 3. Yüzyılda Öklid’in Stoikheia ("Öğeler") adlı yapıtında "aşıt ve ortalama oran" adıyla kayda geçirilmiştir. Eldeki veriler,bu bilginin geçmişinin aslında Eski Mısır’da İ.Ö. 3000 yılına kadar dayandığını göstermektedir. Grek dünyasına da Pythagoras ve Pythagoras’cular tarafından tanıtıldığı ileri sürülür.
Altın oran, (Fi) sayısı olarak bilinir. Bu sayı, Eski Yunan düşünürleri tarafından bulunmuştur, ancak Fi sayısını kimin tanımladığı kesin olarak belli değildir. Eski Yunan düşünürlerinin bazılarının, Fi sayısının yerine (to) sayısını kullandıkları da bilinmektedir.
İ.Ö. 500’lü yıllarda yaşamış olan tüm zamanların en büyük matematikçilerinden biri olan Pisagor , altın oranla ilgili aşağıdaki düşüncelerini dile getirmiştir:
Bir insanın tüm vücudu ile göbeğine kadar olan yüksekliğinin oranı, bir pentagramın uzun ve kısa kenarlarının oranı, bir dikdörtgenin uzun ve kısa kenarlarının oranı, hepsi aynıdır. Bunun sebebi nedir? Çünkü tüm parçanın büyük parçaya oranı, büyük parçanın küçük parçaya oranına eşittir.
Altın oran, günlük yaşantımızda, matematiğin estetik güzelliğe etki ettiği her alanda karşımıza çıkan bir kavramdır. Altın oranın çok çeşitli tanımları verilebilir ama altın oran, neticede matematiksel bir kavramdır ve değeri de 1,618033.... olarak devam eden ondalık bir sayıdır. Altın oranın matematiksel anlamına geçmeden önce altın oranın karşımıza çıktığı bazı alanlara değinelim.
Altın oran, örneğin bir dikdörtgenin göze en estetik gözükmesi için uzun kenarı ile kısa kenarı arasındaki orandır. Buna benzer olarak, bir doğru parçasının ikiye ayrıldığında göze en hoş gelen ikiye ayrılma oranıdır. Altın oran, sadece dikdörtgen ve doğru için değil, neredeyse tüm geometrik cisimler ve yapılar için kullanılabilir.
Altın oranın matematiksel açıdan basit bir tanımı şu şekilde yapılabilir:
Altın oran, 1 sayısına eklendiğinde kendi karesine eşit olan iki sayıdan biridir. Altın oran 1,618033.... olarak devam eden ondalık sayıdır. 1 sayısına eklendiğinde kendi karesine eşit olan diğer sayı da - 0,618033... olarak devam eden ondalık sayıdır.

Altın Oranın Görüldüğü Ve Kullanıldığı Yerler:

	Deniz Kabuğu: Dipten başlayarak uca doğru ilerleyen kıvrımları bulunan deniz kabuğunun, logaritmik spiral denilen her bir kıvrımına oluşan eğikliğin tanjantı altın orana denk gelmektedir.
	El Parmakları: Parmaklarımızın tam orta kısmındaki boğumu, altın oran doğrusundaki B noktası olarak kabul edersek; elimize doğru olan kısa parçanın tırnağımıza doğru olan uzun parçaya oranı ile tırnağa doğru olan uzun parçanın tüm parmağımıza olan oranı eşit olacaktır. Ayrıca büyük parçaların küçük parçalara oranı 1,618′i (Φ) verecektir.
	Kollar: Kolumuz dirseğimizden iki parçaya ayrılmaktadır. Kolumuzda omzumuza doğru olan kısa parçanın elimize doğru olan uzun parçaya oranı ile elimize doğru olan uzun parçanın tüm kolumuzun uzunluğuna oranı eşittir. Ayrıca büyük parçaların küçük parçalara oranı 1,618′i (Φ) vermektedir.
	Çam Kozalağı: Kozalağın içindeki merkez noktadan dışarıya doğru spiral biçiminde uzayan her bir tanenin eğrilik açısı, bizealtın oranı vermektedir.
	Salyangoz: Salyangozların sırtlarındaki sarmal kıvrımlar, onların korunarak büyümeleri için en uygun yöntemdir. Bu sarmal kıvrımlar bir kağıda aktarıldığında bir altın dikdörtgen elde edilmektedir. Yani bunun kısa kenarının uzun kenarına oranı altın orana eşittir.
	Saçtaki Düğüm Noktası: Her insanın kafasının tepe noktasında, saçların çıkmaya başladığı kıvrımlı bir düğüm noktası vardır. Resimde örneklendiği gibi bazı insanlarda bu iki tanedir. Bu düğüm noktasından çıkan saçların yaptığı kıvrım, bir açıyla ilerlemektedir. İşte bu eğimin tanjantı, bize altın oranı vermektedir.
	Tütün: Tütün ve eğrelti otu gibi bazı bitkilerin yaprakları, aşağıya doğru eğimli olarak uzamaktadır. Bu eğimin tanjant değeri altın oranı vermektedir.
	Selimiye Camisi: Mimar Sinan, altın oranı Edirne’deki Selimiye Camisi’nde kullanmıştır. Caminin minarelerindeki ışıklı bölmelerin oranı, altın oranına eşittir. Bu durum Süleymaniye Camisi’nde de geçerlidir.
	İnsan Yüzü: Yüzümüzde altın oranı bulabileceğimiz bir çok yer vardır. Bunlardan biri kaşların arasındaki boşlukla, gözbebekleri arasındaki boşluğun oranıdır. Bunun gibi üst damaktaki ön iki dişin enlerinin toplamının boyların toplamına oranı, 1,618′i vermektedir. Bunlar kuşkusuz standart olarak kabul edilen insan yüzleri için geçerlidir.
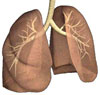	Akciğer: Akciğerlerimizin içinde kas ve bağ dokusundan meydana gelen bronşlar ve bunların sıralı olduğu bronş ağacı bulunmaktadır. İşte bu ağacın dallarının uzunlukları arasındaki oran, altın orana eşittir.
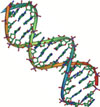	DNA: İnsan vücudundaki en küçük elementlerde bile altın orandan bahsedilmektedir. DNA, düşey doğrultuda iç içe açılmış iki ayrı sarmaldan oluşmaktadır ve bu sarmalların uzunluğu 34 angström, genişlikleri 21 angtröm’dür. 21 ve 34 sayıları, Fibonacci sayı dizisinde arka arkaya gelen iki sayıdır ve bunların birbirine oranı altın orandır.
	Kar Kristalleri: Kristallerin kollarındaki kısa uzantılarla, uzunlar arasında her zaman altın orana uyan bir ölçü bulunmaktadır.
	Geyik Boynuzu: Tıpkı fillerin dişlerindeki sarmal yapılarda olduğu gibi, geyiklerin boynuzlarındaki çıkıntılarda da, 1,618′lik altın oran bulunmaktadır.
	Mısır Piramitleri: Milattan önce yapıldığı düşünülen bir yapı olduğu bilinmesine rağmen, altın oranı birebir görebildiğimiz Keops Piramidi’nin taban uzunluğu ile yüksekliğinin birbirine oranı altın oranı vermektedir.
	Mona Lisa Tablosu: Leanardo da Vinci tarafından yapılan Mona Lisa tablosunun boyu ile eni arasındaki oran, altın orana eşittir. Tıpkı Aziz Jerome tablosundaki gibi… Ayrıca Picasso da aynı ölçüyü resimlerinde kullanmıştır.
	Ayçiçeği: Tıpkı papatyadaki gibi, çiçeğin merkezinden sağa doğru gidenlerle sola doğru giden taneciklerin oranı altın orana eşittir. Papatyaya benzeyen çiçeklerin neredeyse tamamında bu oran geçerlidir.

Hülya’nın güzelliğine bilimsel onay

31.05.2000

Hülya Avşar’ın güzel bir kadın olduğunu zaten herkes kabul ediyor. Avşar’ın güzelliğine bir onay da bilim dünyasından geldi. Çukurova Üniversitesi’nden iki profesör, ‘Ortodontide Sefalometri’ adlı bilimsel kitapta Hülya Avşar’ın güzelliğini tescil etti. Profesör Doktor İlter Uzel, ‘Sanatçımızın yüz güzelliği bilimsel anlamda kusursuz çıktı’ dedi.

ÇUKUROVA Üniversitesi Diş Hekimliği Fakültesi Dekanı Prof.Dr. İlter Uzel'in, Hacette Üniversitesi Diş Hekimliği Fakültesi Öğretim Üyesi Prof.Dr. Ayhan Enacar'la birlikte yayımladığı ‘‘Ortodontide Sefalometri’’ adlı bilimsel kitapta Hülya Avşar'ın güzelliği bilimsel anlamda da tescil edildi. İki profesör de Türkiye’nin en güzel kadınları arasında gösterilen Hülya Avşar’ın özellikle yüzünün Eski Mısır’dan bu yana bilinen ‘Altın Oran’a tıpatıp uyduğu nu söylediler.

YÜZÜ MÜKEMMEL

Kitabına, Avşar kızını model olarak alan ve bir fotoğrafından yüz hatlarını heykeltraşlar ve mimarlar tarafından da kullanılan ‘Altın Oran’’ tekniğiyle değerlendiren Prof.Dr. Uzel, ‘‘Sanatçımızın yüz güzelliği bilimsel anlamda kusursuz çıktı.

Avşar'ın ağzı, burnu, yanakları, alnı, çenesi ve gözleri tamamen birbirine orantılı yaratılmış.

Afrodit gibi kusursuz bir güzelliğe sahip olduğunu söyleyebilirim’’ dedi.

DOĞADAKİ GERÇEK

İnsanlığın Helenistik çağ heykelleri ve mimariden çağdaş eserlere ya da güzellik tanrıçası Afrodit'ten popüler kültür starlarına uzanan bir çizgide hep ortak bir estetik anlayışı olduğunu belirten Prof. Dr. Uzel, kitabın bir bölümünde de insan vücudundaki organların estetik açıdan birbirleriyle olan oranını ele aldıklarını söyledi.

Eski Mısırlılar'dan buyana bilinen ‘Altın Oran’ ölçüm tekniğinin insan aklından çıkan bir tasarım değil, doğada var olan biyolojik bir gerçek olduğunu belirten Prof.Dr. Uzel, şöyle konuştu:

‘‘Örneğin yaprak damarlarının birbirini izleyişi hep altın oranı vermektedir.

ALTIN ORAN

Uyumlu bir estetiğe sahip insan yüzünde de altın oranların varlığı Leonardo da Vinci, ya da Dürer döneminden beri bilinmektedir. Altın oranlar klinik muayene sırasında bir Altın Pergel'le direkt olarak değerlendirilebileceği gibi, fotoğraf üzerinde de ölçülerek elde edilebilir. Altın Oran'ın belirlenmesi için kullanılan Altın Pergel'in kolları her zaman için Altın Oranı koruyacak şekilde açılır.’’